Table of Contents
1. Bất đẳng thức Bunhiacopxki và ứng dụng trong toán học

Bất đẳng thức Bunhiacopxki là một bất đẳng thức rất quen thuộc và được ứng dụng rất nhiều trong các bài toán về bất đẳng thức và cực trị. Nó có khả năng xác định giới hạn trên hoặc dưới của một biểu thức, từ đó giúp chúng ta tìm ra giá trị lớn nhất hoặc nhỏ nhất của biểu thức đó.
Bất đẳng thức Bunhiacopxki có nhiều dạng khác nhau, nhưng dạng cơ bản của nó được biểu diễn như sau:
Đối với hai bộ số a1, a2,…, an và b1, b2,…, bn, ta có:
(a1^2 + a2^2 +… + an^2)(b1^2 + b2^2 +… + bn^2) ≥ (a1b1 + a2b2 +… + anbn)^2
Trong toán học, chúng ta có thể áp dụng bất đẳng thức Bunhiacopxki để giải các bài toán về tìm giá trị lớn nhất hoặc nhỏ nhất của một biểu thức. Chẳng hạn, trong các bài toán về tìm giá trị cực trị của hàm số, ta có thể sử dụng bất đẳng thức Bunhiacopxki để chứng minh tính chất cực trị của điểm cực trị.
Với ứng dụng linh hoạt và rộng rãi trong toán học, bất đẳng thức Bunhiacopxki là một công cụ hữu ích giúp chúng ta hiểu và giải quyết các vấn đề liên quan đến bất đẳng thức và cực trị.
2. Tên gọi chính xác của bất đẳng thức Bunhiacopxki và người phát hiện
Bất đẳng thức Bunhiacopxki có tên gọi chính xác là bất đẳng thức Cauchy – Bunhiacopxki – Schwarz, được phát hiện và đề xuất bởi ba nhà toán học độc lập. Người Nga Bunhiacopxki là một trong ba nhà toán học đã phát hiện ra bất đẳng thức này.
3. Tên gọi khác của bất đẳng thức Bunhiacopxki và người đề xuất
Bất đẳng thức Bunhiacopxki còn có tên gọi khác là bất đẳng thức Cauchy-Schwarz hoặc bất đẳng thức CS. Bất đẳng thức này được các nhà toán học Cauchy, Bunhiacopxki và Schwarz phát hiện ra và công nhận.
4. Bản quyền tài liệu về bất đẳng thức Bunhiacopxki thuộc về ai?
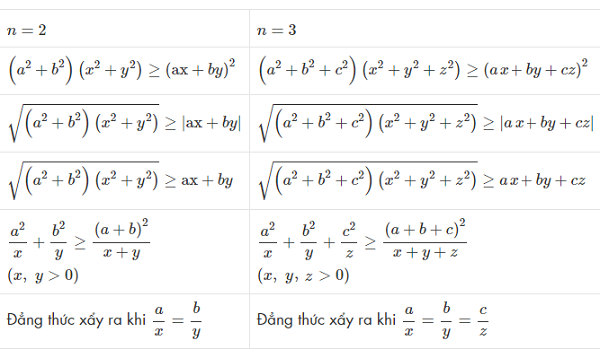
Các tài liệu về bất đẳng thức Bunhiacopxki thuộc về VnDoc, một tổ chức đã biên soạn và sở hữu quyền tài liệu này.
5. Áp dụng bất đẳng thức Bunhiacopxki trong giải các bài toán về bất đẳng thức và cực trị
Bất đẳng thức Bunhiacopxki rất quan trọng và được ứng dụng rộng rãi trong giải các bài toán về bất đẳng thức và cực trị. Nó giúp chúng ta xác định được giới hạn của một biểu thức số học, từ đó tìm ra giá trị lớn nhất hoặc nhỏ nhất của biểu thức đó.
6. Quy ước khi một số i trong hai bộ số a và b bằng 0 – ví dụ minh hoạ

Quy ước khi một số i trong hai bộ số a và b bằng 0 là nếu một số i nào đó (i = 1, 2, 3, …, n) trong hai bộ số a và b có giá trị là 0, thì tương ứng với nó ta có giá trị là 0.
Ví dụ minh hoạ:
Cho hai bộ số a = (1, 2, 3) và b = (4, 5, 0). Ta có:
a.b = (1*4) + (2*5) + (3*0) = 14.
Trong ví dụ này, khi i=3 ta có biến của bộ số a là khác không, nhưng biến của bộ số b là bằng không.
Tổng kết, bất đẳng thức Bunhiacopxki là một công cụ quan trọng trong toán học và được áp dụng rộng rãi trong nhiều lĩnh vực. Nó giúp chúng ta xác định mối quan hệ giữa các biểu thức số học và áp dụng để giải quyết các bài toán khác nhau. Bằng cách hiểu và sử dụng bất đẳng thức Bunhiacopxki, chúng ta có thể tăng cường khả năng phân tích và suy luận trong việc giải quyết các vấn đề liên quan đến số liệu.

