Table of Contents
Làm thế nào để tính độ dài đường chéo của một hình thoi?
Để tính độ dài đường chéo của một hình thoi, ta có thể sử dụng công thức tính toán dựa trên các cạnh của hình thoi. Đối với một hình thoi có cạnh a, ta có công thức tính đường chéo như sau:
đường chéo = a * √2
Trong công thức này, a là độ dài của cạnh và √2 là căn bậc hai.
Đường chéo của hình thoi là đường nối như thế nào?
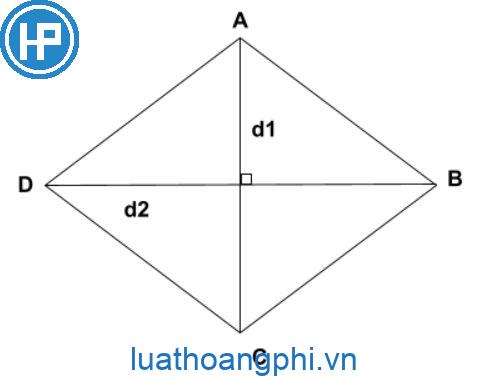
Đường chéo của hình thoi là đường nối hai đỉnh đối diện của hình thoi. Nó đi từ góc này qua tâm của hình thoi và kết thúc ở góc đối diện. Điểm giao nhau giữa hai đường chéo được gọi là trung điểm của hình thoi và cũng là tâm của nó.
Hai đường chéo trong hình thoi có bằng nhau không?
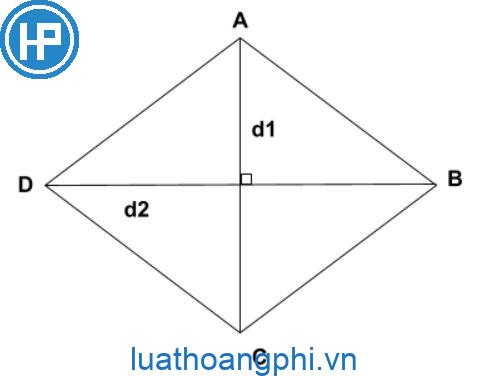
Có, hai đường chéo trong một hình thoi có bằng nhau. Hai đoạn reo này cắt nhau tại trung điểm và tạo thành một góc vuông.
Đường chéo của hình thoi cắt nhau ở đâu?
Đường chéo của hình thoi cắt nhau tại trung điểm của hình thoi. Điểm giao nhau giữa hai đường chéo được gọi là trung điểm và cũng là tâm của hình thoi.
Hình thoi có bao nhiêu đặc điểm đối xứng?
Hình thoi có ba đặc điểm đối xứng. Đó là:
1. Đối xứng qua trục qua tâm: Hình thoi có một trục đối xứng qua tâm của nó, nghĩa là nếu ta vẽ một đường thẳng đi qua tâm của hình thoi, hình thoi sẽ được chia thành hai phần đối xứng.
2. Đối xứng qua một trong hai đường chéo: Mỗi đường chéo trong hình thoi cũng là một trục đối xứng, chia hình thoi thành hai nửa đối xứng.
3. Đối xứng qua các cạnh: Các cạnh trong hình thoi cũng là các trục đối xứng, chia hình thoi thành các phần symmetrical.
Trong bài viết này, chúng ta đã tìm hiểu về cách tính đường chéo hình thoi. Để tính được đường chéo hình thoi, ta có thể sử dụng công thức Pythagoras hoặc công thức Heron. Qua các ví dụ và giải thích chi tiết, chúng ta đã nắm bắt được quy trình tính toán một cách dễ dàng và hiệu quả. Việc tính đường chéo hình thoi không chỉ giúp chúng ta hiểu rõ về hình học mà còn có ứng dụng trong nhiều lĩnh vực khác nhau như xây dựng, thiết kế hay khoa học tự nhiên.