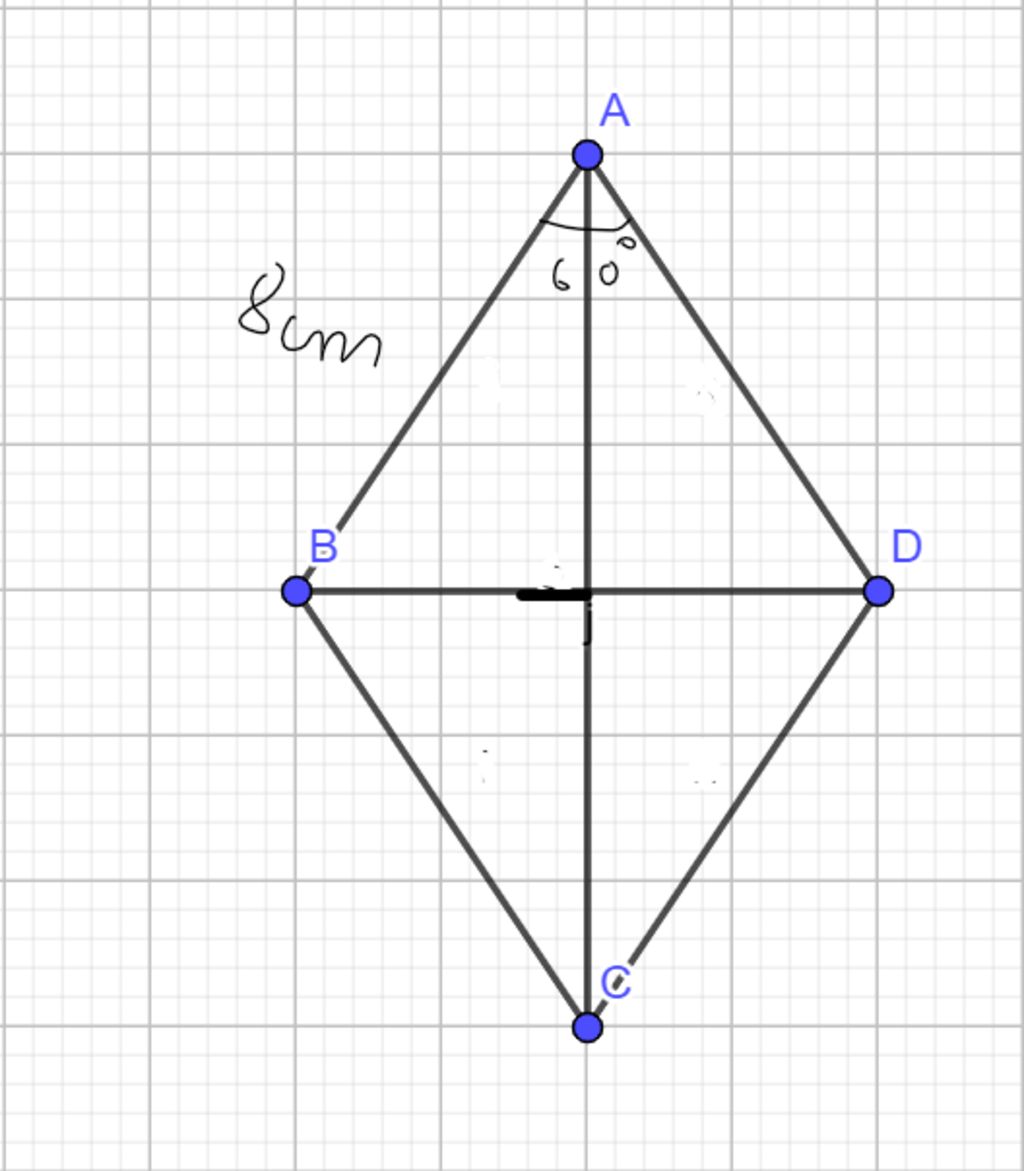
1. Tính chất của hình thoi có góc 60 độ là tạo ra hai đường chéo vuông góc với nhau và chúng cắt nhau tại một điểm. Điểm này được gọi là giao điểm.
2. Góc 60 độ trong hình thoi tạo ra đường chéo vuông góc nhau tại một điểm, cụ thể là giao điểm của hai đường chéo. Điểm này được xem như trung điểm của các cạnh của hình thoi.
3. Điểm giao của hai đường chéo trong hình thoi được gọi là giao điểm vì nó là điểm duy nhất mà hai đường chéo cắt nhau và tạo thành một điểm trung tâm cho hình thoi. Điểm này cũng là trung điểm cho các cạnh của hình thoi.
4. Tính chất khác nhau giữa hình thoi và hình vuông là:
– Hình thoi có các cạnh bằng nhau, trong khi hình vuông có các cạnh và các góc bằng nhau.
– Hình vuông có 4 góc vuông, trong khi hình thoi không có.
– Hai đường chéo trong hình vuông bằng nhau và cắt nhau ở trung điểm, trong khi hai đường chéo trong hình thoi không bằng nhau và cắt nhau ở một điểm không phải trung điểm.
5. Cách chứng minh một hình tứ giác là hình thoi có thể được thực hiện bằng cách chứng minh các tính chất sau:
– Hình tứ giác có 4 cạnh bằng nhau.
– Hai đường chéo của hình tứ giác vuông góc và cắt nhau tại một điểm.
– Hai đường chéo cắt nhau ở trung điểm của các cạnh của hình tứ giác.
Table of Contents
1. Tính chất của hình thoi có góc 60 độ là gì?

Trong hình thoi, nếu một trong các góc của nó có giá trị bằng 60 độ, thì tất cả các góc khác cũng sẽ có giá trị bằng 60 độ. Điều này do tính chất đặc biệt của hình thoi là tứ giác có các cạnh bằng nhau và các đường chéo vuông góc với nhau. Vì vậy, khi một góc trong hình thoi có giá trị 60 độ, thì tất cả các góc khác cũng sẽ có giá trị này.
2. Góc 60 độ trong hình thoi tạo ra đường chéo vuông góc nhau ở đâu?
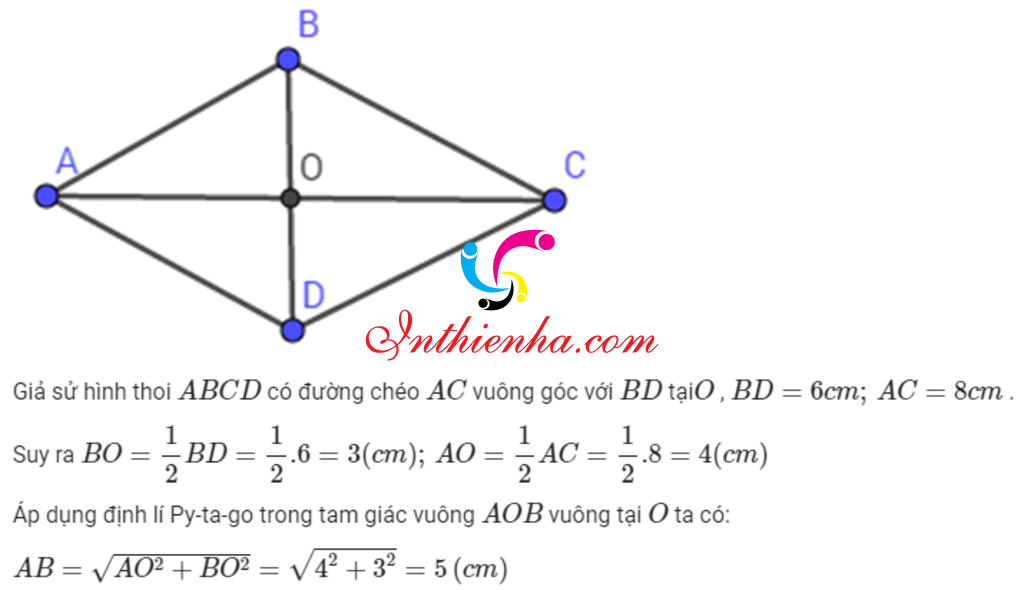
Trong hình thoi, hai đường chéo được tạo ra từ các góc của nó. Điểm nối hai đường chéo lại với nhau được gọi là điểm giao hay tâm của hình thoi. Nhờ tính chất riêng biệt này, ta biết rằng hai đường chéo trong hình thoi luôn luôn vuông góc với nhau.
3. Vì sao điểm giao của hai đường chéo trong hình thoi được gọi là giao điểm?
Điểm giao của hai đường chéo trong hình thoi được gọi là giao điểm vì nó là điểm duy nhất mà hai đường chéo này cắt nhau. Điểm này cũng là trung điểm của cả hai đường chéo và đồng thời là tâm của hình thoi. Từ tính chất này, ta có thể sử dụng điểm giao để xác định các phép biến đổi và tính toán trong hình thoi.
4. Tính chất khác nhau giữa hình thoi và hình vuông là gì?
Hình thoi và hình vuông đều là tứ giác có các cạnh bằng nhau, tuy nhiên có một số tính chất khác nhau. Đầu tiên, hình vuông có tất cả các góc bằng 90 độ, trong khi hình thoi không nhất thiết có các góc bằng 90 độ. Thứ hai, hai đường chéo của hình vuông luôn cắt nhau vuông góc tại trung điểm của chúng, trong khi hai đường chéo của hình thoi luôn cắt nhau vuông góc và qua tâm của hình thoi.
5. Cách chứng minh một hình tứ giác là hình thoi?
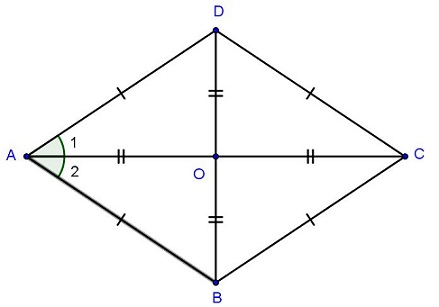
Để chứng minh một tứ giác là hình thoi, ta cần sử dụng các tính chất đặc biệt của hình thoi. Có tổng cộng 6 cách chứng minh hình thoi, bao gồm:
1. Chứng minh rằng tứ giác có các cạnh bằng nhau và hai đường chéo cắt nhau vuông góc tại điểm giao.
2. Chứng minh rằng tứ giác có hai cạnh liền kề bằng nhau và các đường chéo qua trung điểm của các cạnh này là vuông góc với nhau.
3. Chứng minh rằng tứ giác là hình bình hành và có một góc vuông.
4. Chứng minh rằng tứ giác có một cặp đường phân giác bằng nhau và hai góc nằm liền kề bằng nhau.
5. Chứng minh rằng tứ giác có hai khối đối xứng qua các đường phân giác của nó.
6. Chứng minh rằng tứ giác có hai khối đối xứng qua hai trục đối xứng của nó.
Tính chất hình thoi có góc 60 độ đã được nghiên cứu và phân tích trong bài viết này. Chúng ta đã thấy rằng, hình thoi có góc 60 độ là một loại hình tứ giác đặc biệt với những đặc điểm đáng chú ý như các cạnh bằng nhau, các góc trong bằng 60 độ và tổng các góc là 360 độ. Điều này giúp cho hình thoi có ứng dụng rộng rãi trong nhiều lĩnh vực như xây dựng, thiết kế và toán học. Tìm hiểu về tính chất này sẽ giúp chúng ta hiểu sâu hơn về hình thoi và áp dụng vào các bài toán thực tế.